USB Charger QC3 4 port charger KeKe-QC-04



Official specifications:

• Input voltage: 100-240 V 50-60Hz
• Output: 5 V / 3 A (max.)
• Support QC3

I got it from ebay dealer: nctqkj2-2017



No fancy packing for this, just a white plastic envelope with the charger in it, no accessories or instruction sheets.










Measurements

• Power consumption when idle is 0.23 watt
• Regular USB outputs are coded as USB charger (DCP)
• Regular USB outputs are in parallel.
• QC output is coded as Apple 2.4A, DCP, QC3, Samsung-AFC, Huawei-FCP
• Minimum QC3 voltage is 3.7V
• There is a blue LED behind the USB connectors
• Weight: 55.1g
• Size: 88.3 x 45.1 x 26.9mm

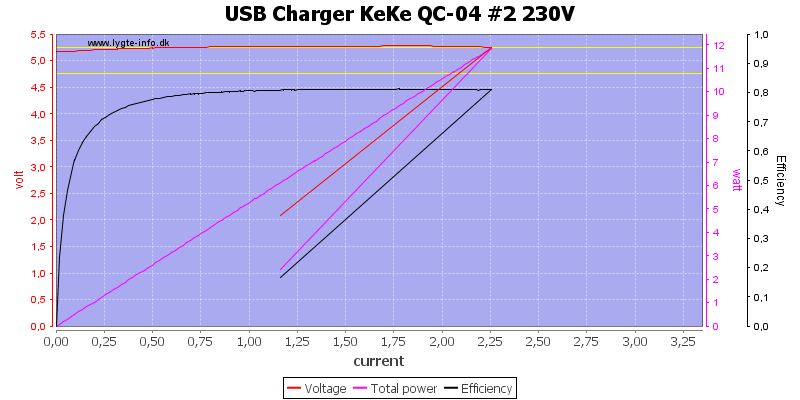
A single output can deliver 2.25A



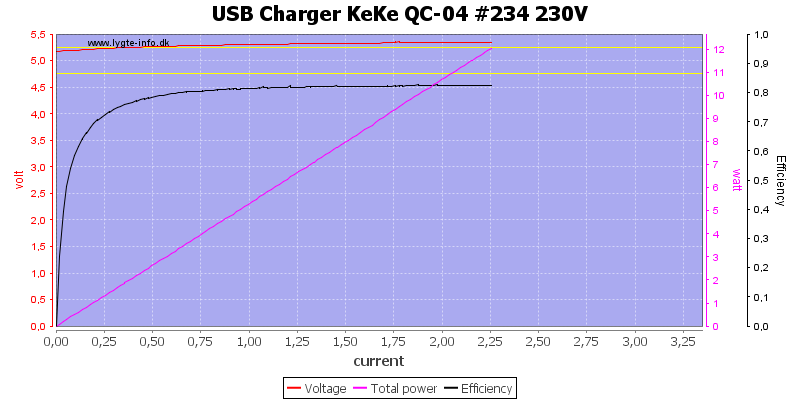
Using all 3 regular USB outputs together has the same limit.



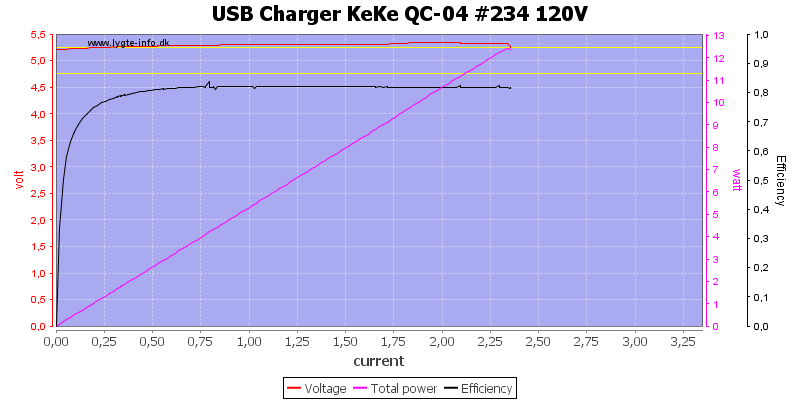
The limit is slightly higher at 120VAC.



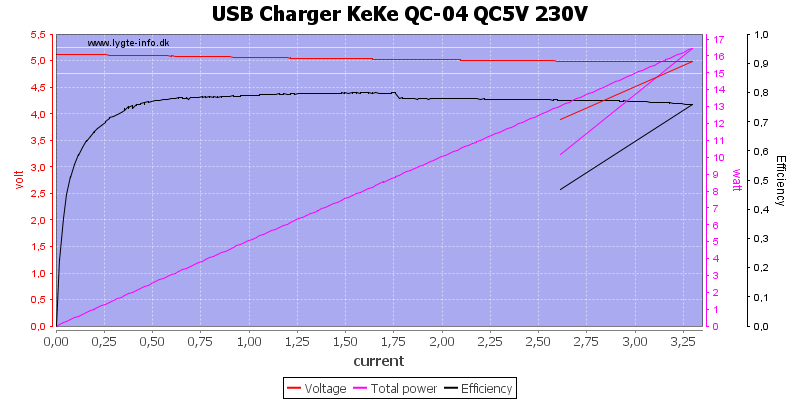
The QC output can deliver 3.2A at 5V.



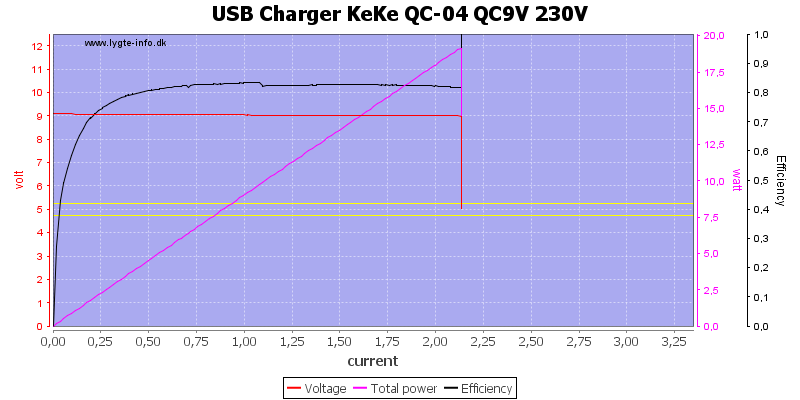
And about 2.2A at 9V



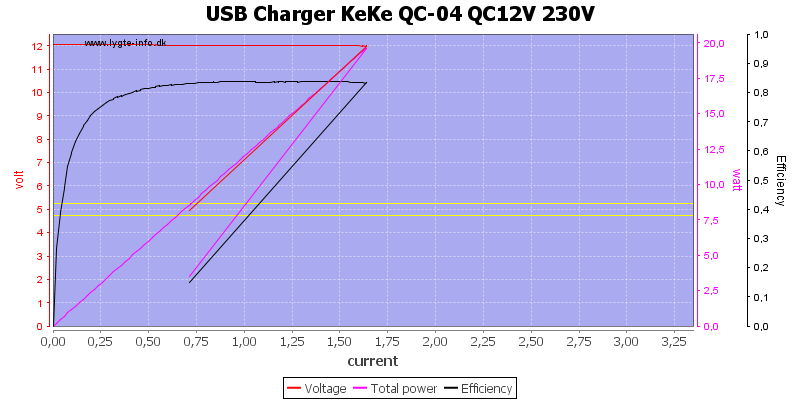
And 1.6A at 12V



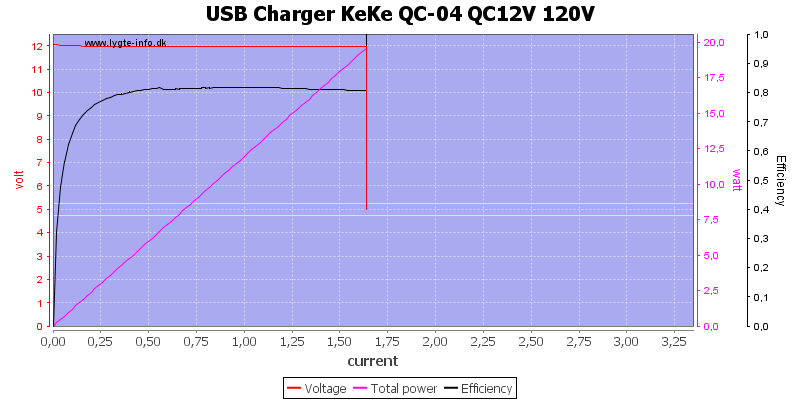
There is not much difference with 120VAC supply.



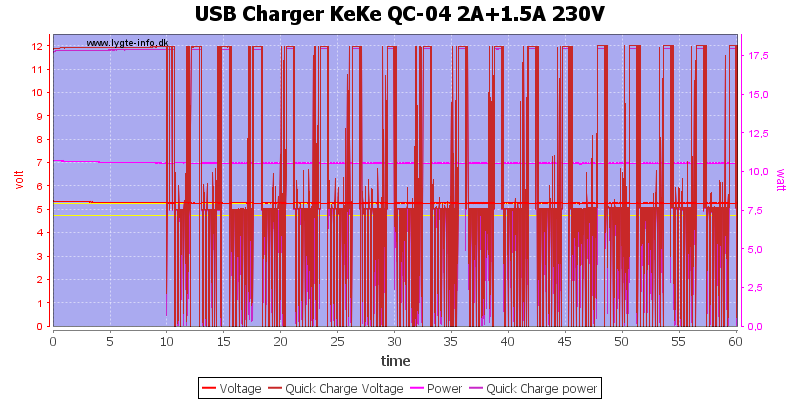
Load the supply with 2A on 5V and 1.5A on QC 12V worked for 10 minutes, then the QC output needed to rest.



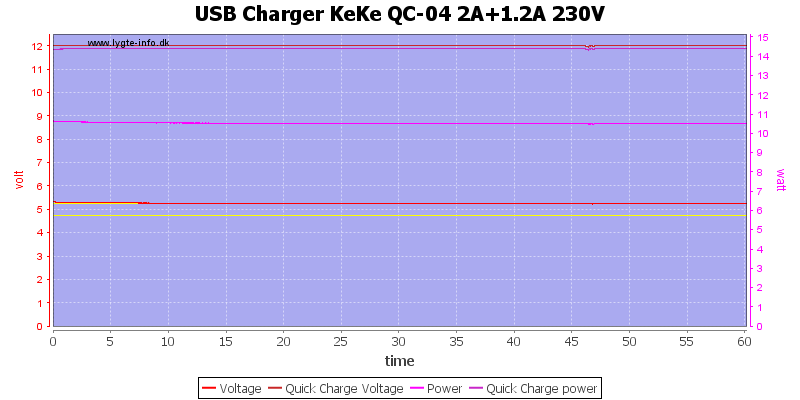
Reducing the load to 1.2A on the QC output worked better and I could run a 1 hour test.
The temperature photos below are taken between 30 minutes and 60 minutes into the one hour test.



M1: 45.2°C, M2: 55.5°C, HS1: 79.2°C
HS1 is probably the input smoothing capacitor that is transferring heat to the enclosure.



HS1: 83.0°C
Here HS1 is the 5V transformer.



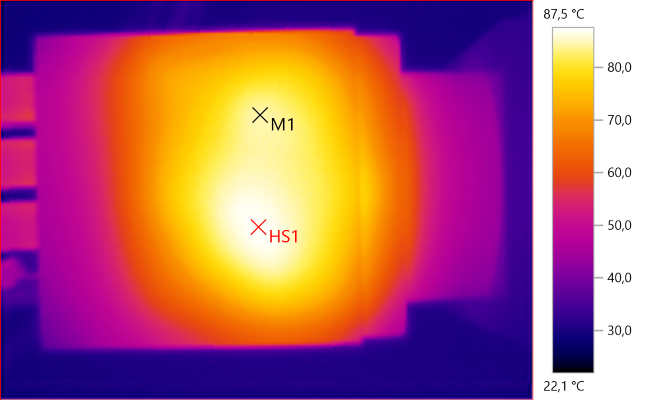
M1: 84.5°C, HS1: 87.5°C
HS1 is QC transformer and M1 is 5V transformer.



HS1: 73.1°C



M1: 60.6°C, HS1: 78.4°C



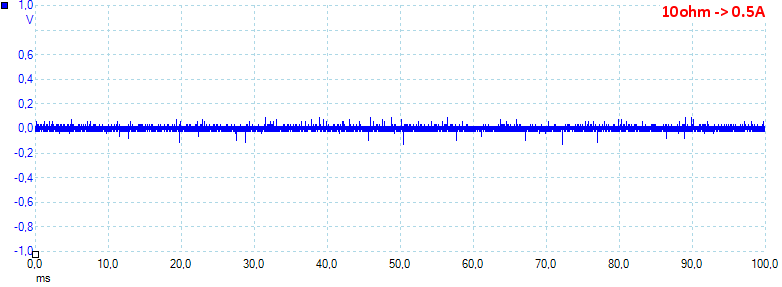
At 0.5A the noise is 26mV rms and 542mVpp.



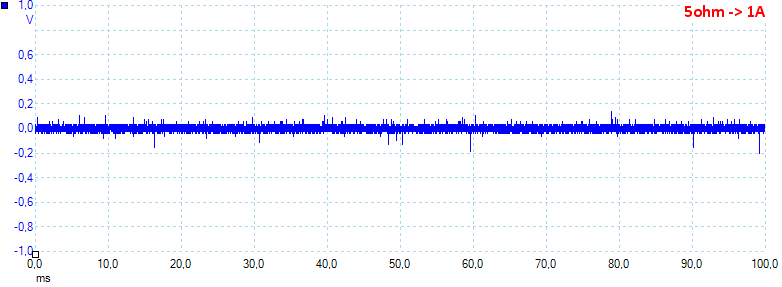
At 1A the noise is 27mV rms and 410mVpp.



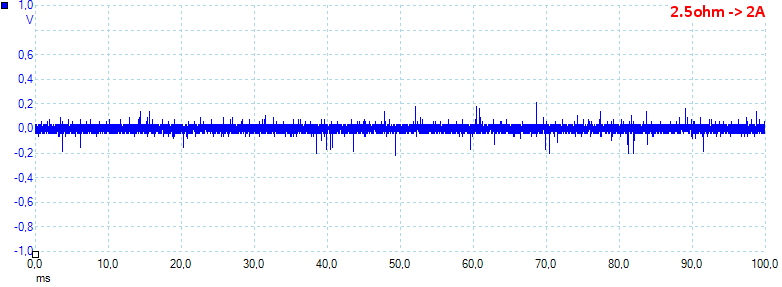
At 2A the noise is 57mV rms and 582mVpp.



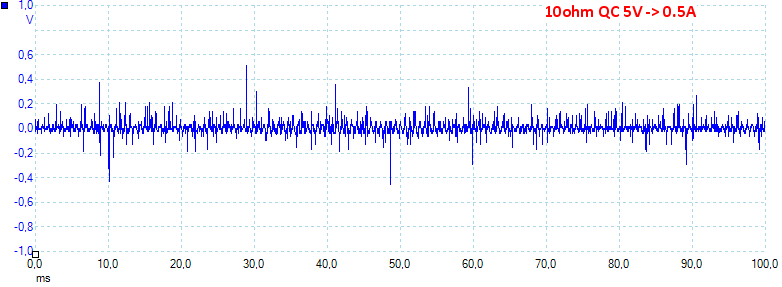
At 0.5A QC 5V the noise is 45mV rms and 1382mVpp.



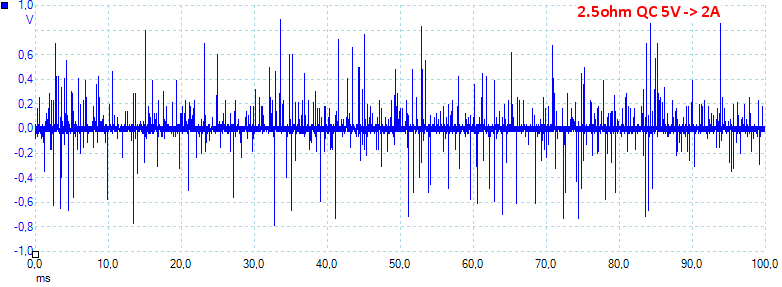
At 1A QC 5V the noise is 70mV rms and 1683mVpp.



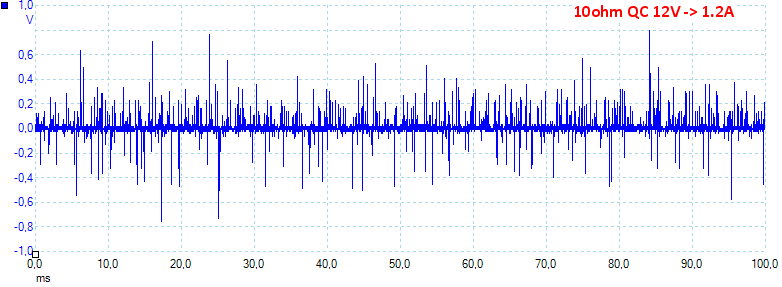
At 1.2A QC 12V the noise is 71mV rms and 1913mVpp. The RMS noise is fairly low, but the switcher has a lot of common mode noise that shows in the pp noise.




Tear down



I could open it the usually way by mounting the base in a vice and whacking the top with a mallet, but the glue was fairly strong.



With charger that can do multiple USB outputs with different voltages it is always interesting to see how the do it, here they use two mains transformers, one for QC and one for regular 5V.
At the input is a fusible resistor (F1), the QC switcher is on this side (HC2502), between the two transformers is the "safety" capacitor and on the other side of the QC transformer is a opto-coupler for feedback.







On this side is a lot of electronic, there is the bridge rectifier at the input (ABS210), the switcher for 5V (HC2511: 10 Watt) with a synchronous rectifier (HC7703S) on the low volt side, The QC part uses a rectifier diode (U5: ST10100), the QC controller is a 6 pin chip (U6: HC66020) with the support of a reference (U7: 431)





With two power supplies in a small box it is difficult to get enough safety distance between mains and low volt side. I am not sure I have found the worst location, but here is about 3mm this is about half of the required distance.



The charger passed the 2830 volt test, but failed the 4242 volt test between mains and low volt side, this makes it unsafe for 230VAC countries.



Conclusion

Both safety and 5V output power is bad on this charger. A total of about 2A for 3 USB outputs is way to low. The lack of isolation distance is bad.



Notes

Index of all tested USB power supplies/chargers
Read more about how I test USB power supplies/charger
How does a usb charger work?