Charger Opus BT-C700





This is a compact 4 channel analyzing charger from Opus.




I got the charger in a cardboard box.



The box contains the charger, a power supply and a manual.



The charger has a barrel connector for 12V power input.



As all analyzing charger it has a display and a couple of buttons.



When powered on the charger briefly shows the version number of the software.



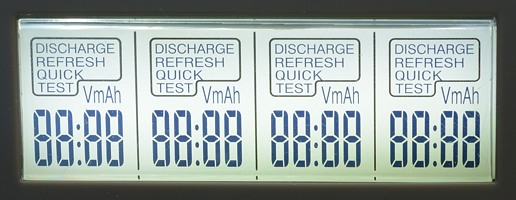
Selftest during powerup shows all the text on the display.



When working the display looks like this, the DISPLAY button can be used to select what to show (v/h/mA/mAh).
The MODE button is used to select mode for one or for all slots, it is also possible to change mode later on.
The CURRENT button will step between the possible currents.




The charger uses a AA/AAA two level slot. Notice the metal strips touching the side of the battery, this is probably connected to a temperature sensor.







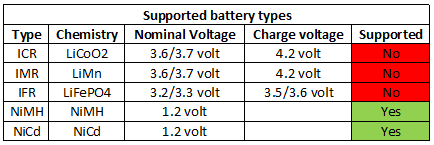
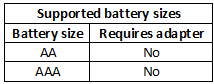
Measurements

• When not powered it will discharge the battery with 0.4mA
• Charge will restart charging after power loss, or battery insertion.

Charge

The charge mode can select between 200, 300, 400, 500, 700 and 1000, default is 400mA. The 1000mA is only available in slot #1 and #4 and only when slot #2 and #3 is empty.



The charger reduces current when the battery is nearly finished, this keeps the heat down, but makes it more difficult to terminate correctly. This charger is smart enough to terminate correctly even at the lower current.
Display shows 2027mAh in 3:20





The same with the 3 other slots, all have nice terminations.
Display shows 2049mAh, 2020mA, 2030mA in 3:28, 3:18, 3:23



Even at 200mA current the charger do a nice termination.
Display shows 1849mAh in 9:27



With 400mA the current is high enough to see the increased temperature when the cell is full.
Display shows 2052mAh in 5:53



The charger is rated to do 1A, but it is at the limit.
Display shows 2078mAh in 2:29



The charger needs some time to reconize a full cell, but it is smart enough to do it at low current.
Display shows 190mAh in 0:22



This XX is also fully charged.
Display shows 2076mAh in 2:52



Same with the Pro.
Display shows 2623mAh in 3:07



For some reason the 1A charge current is slightly lower here, but the cell is perfectly charged.
Display shows 2553mAh in 3:15



The AAA is no surprise, also perfectly charged.
Display shows 790mAh in 2:00



With four cells the maximum charge current is 700mA and it is handled fine (Remember my temperature sensor is not mounted on the same cell as the V/A sensors).
Display shows 1944mAh, 2091mAh, 2032mAh, 2091mAh in 3:06, 3:21, 3:15, 3:20



The charger uses below 1A from 12V.



M1: 43,6°C, M2: 47,4°C, M3: 48,3°C, M4: 44,4°C, M5: 51,5°C, M6: 32,6°C, HS1: 58,9°C

With the compact size the temperature is a bit high at full charge current.



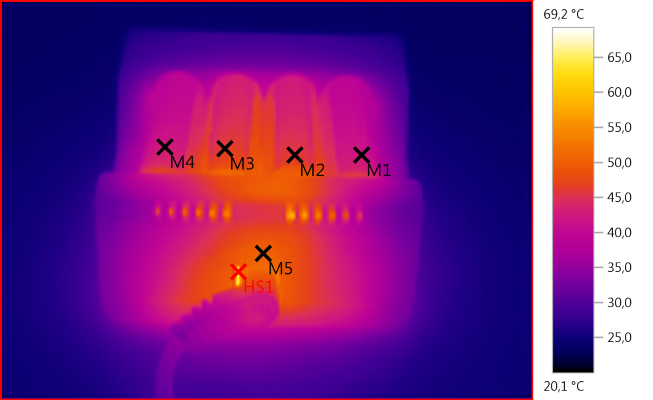
M1: 42,1°C, M2: 46,1°C, M3: 46,2°C, M4: 42,5°C, M5: 50,6°C, HS1: 69,2°C



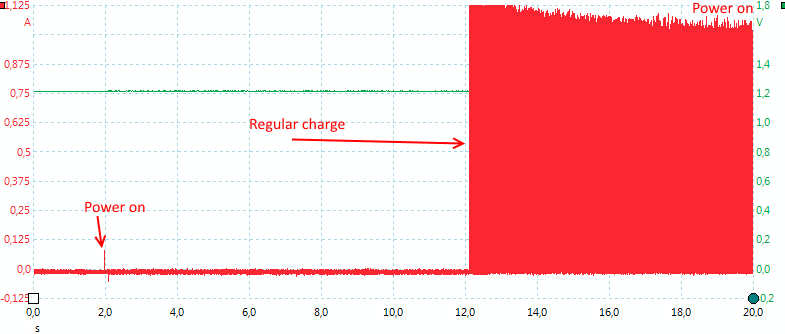
The charger is a bit slow to start, because it is waiting some seconds for user input.



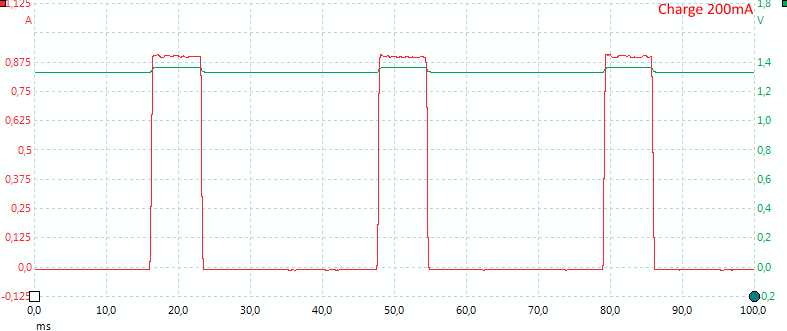
Charge current is regulated with pwm.



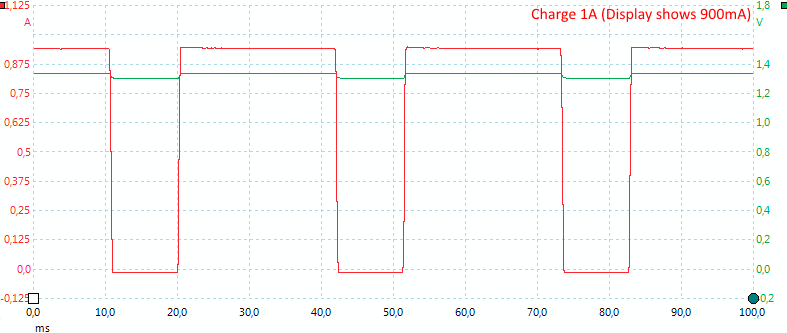
Here I have selected maximum charge current, but due to my sense equipment (0.1ohm resistor in series with battery) the charge cannot reach full current.



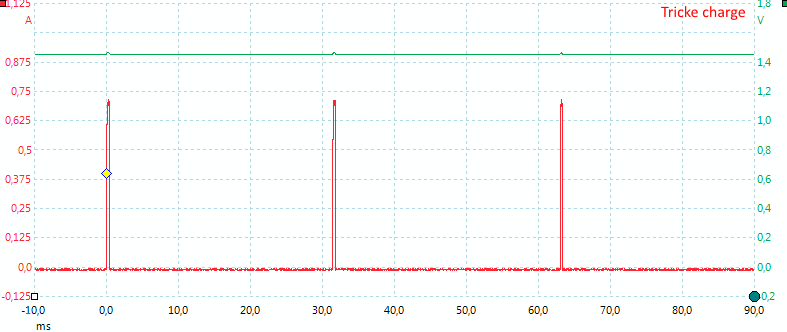
Trickle charge is done with a current spikes each 30 second.



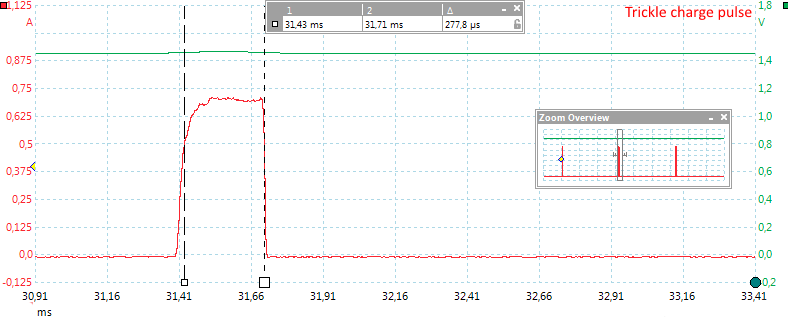
The spike is 0.0003 second long.



Discharge

The discharge mode can select between 100, 200, 300, 400 and 500mA, default is 300mA



The discharge is to somewhere between 0.8 and 0.9 volt.
Display shows 1855mAh in 3:44



A 100mA discharge takes a lot of time.
Display shows 1931mAh in 19:23



Discharging four cells at once will heat the charger.
Display shows 1895mAH, 1980mAh, 1977mAh, 1980mAh in 3:39, 3:59, 3:50. 3:59



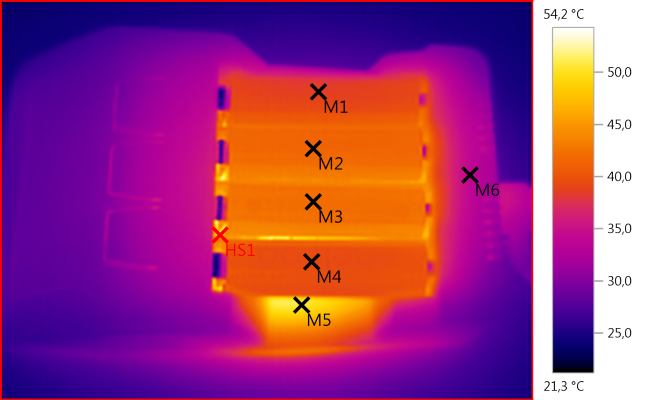
M1: 38,7°C, M2: 41,5°C, M3: 42,1°C, M4: 39,2°C, M5: 50,5°C, M6: 34,1°C, HS1: 54,2°C
Discharge do also generate some heat, but not as much as charging.



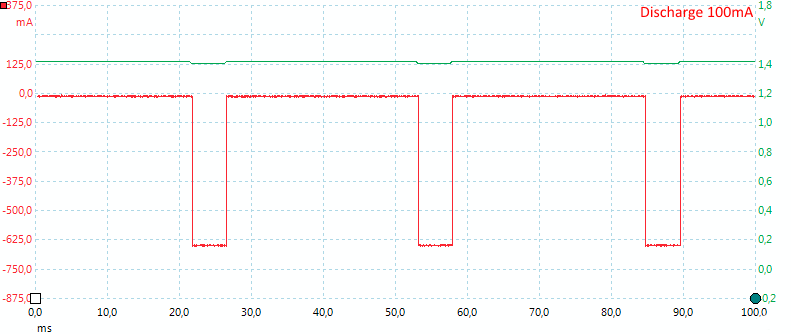
Discharge is also done with pwm, above curve is lowest current.



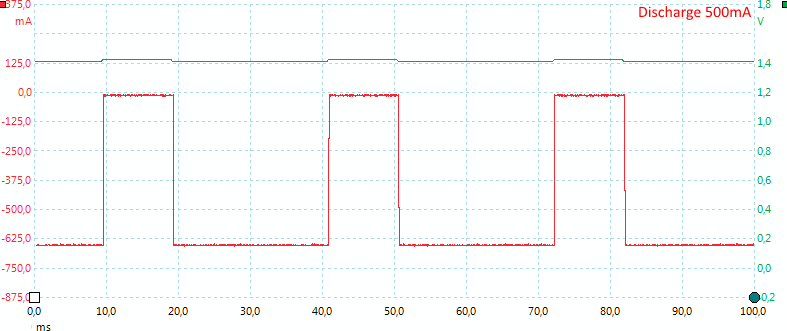
Highest discharge current.



Discharge Refresh

This function will cycle the cell a couple of times, it finish with a charged cell.



Display shows 1904mAh in 2:30



Charge Test

This function will charge the battery, discharge the battery and then charge it again. The display will show the discharge capacity and time.



Looks like two nice charge curves with the discharge between.
Display shows 1948mAh in 2:28



Quick test

This function measures the internal resistance of the battery, this is an indication of how well the battery performs (Lower value is better).




First line shows the reading when I just put the battery in the charger.
The second line shows the reading when connected to my test equipment, but without extra resistance.
+10, +40 and +100 means I have added that much resistance (Tolerance is only a few mOhm), the result is supposed to show these values.
All tests are done with the same battery.

The charger gets wrong result frequently when I am using my test rig. I suspect that my test rig is affecting the charger.




Replacing the wrong result with the value from an adjacent column makes the result look very good.



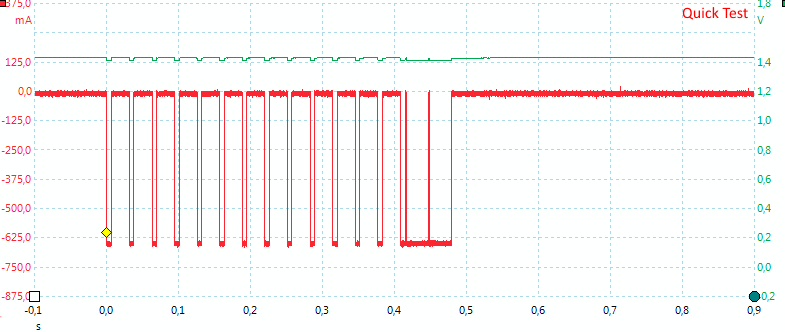
The charger load the battery a bit before doing the actual measurement.



Testing the mains power supply with 2500 volt and 5000 volt between mains and low volt side, did not show any safety problems.



Conclusion

This is a compact analyzing charger and this means it will run a bit on the warm side when using full current. The charge algorithm is a bit special with the lower charge current when the battery is nearly full, but it works well and do keep the final temperature lower.

All functions works as expected, the user interface is easy to use and it was not early or late on a single termination, this makes it a good NiMH charger.



Notes

The charger was supplied by gearbest for a review.
I have tested two copies of this charger, the first one was faulty and would not terminate when using lower charge currents!

Here is an explanation on how I did the above charge curves: How do I test a charger