Charger Xtar XP4





Xtar is known for flashlights and a couple of good LiIon chargers. This time they have also included NiMH capabilities in the charger and together with 3 current settings and USB output it looks like a charger that can do just about everything (Except analyze).






The charger comes in a cardboard box with lots of specifications on the outside.



The box contains the charger, a mains adapter, a car adapter (Probably optional), a manual and a warranty card.



The front/top of the charger contains 8 leds and one button:

• 3 blue leds to show the charger current, a short press on the button will select next charge current.
• 1 blue usb led, this led will be on when the usb output is active. To activate the output slot #4 must have a charged LiIon battery, power must be disconnected and the button must be pressed for some time.
• 4 red/green status leds. They are red when charging and green at other times. When slot #1 is discharging the led will flash red (Activated by a long press on the button).

The charger has a 12 volt input, this input can be supply from the main adapter or from the car adapter.
The usb output is rated at 1A and uses the battery in slot #4. It can only be activated when input power is disconnected.



Xtar uses this label to avoid fakes.



The battery + connection is slightly raised and worked with flat top batteries. The slider works fine.
The slider can work with batteries between 30.5 mm and 71.8 mm.








The charger can easily handle 70 mm long batteries, including flat top cells. (See my Small LiIon comparison for length of different brands).


Measurements charger

• When not connected to power it will discharges with up to 0.6mA, except slot #4 for usb output, it will discharge with up to 11mA.
• When power is connected with a full battery, the charger will charge with 170uA (All slots with LiIon).
• When power is connected with a full battery, the charger will charge with 10mA/30mA/50mA trickle charge (All slots with NiMH).
• At 0 volt on the battery the charge current is 1.6mA (Green led is on).
• At 0.22 volt the red led turns on and the current jumps to 90mA
• At 1.22 volt the full charge current is turned on for NiMH.
• At about 3 volt the full charge current is turned on for LiIon.
• Any voltage drop, reinsertion of battery or power cycling will restart charging.
• The led is flashing red when discharging. This only works on channel #1.
• The channels on the charger are independent, i.e. there are small differences between them.

Test with LiIon cells



Charging a 3100mAh cell with 0.25A is slow, but works perfectly. Notice the low terminations current, this is good. Lower would be even better, when charging small batteries.



Increasing the current to 0.5A does also look good. The termination current has increased slightly.



At 1A is also good, the termination current is about 100mA which is fine.





The other slots works just as well.



The charge time for 2600mAh is slightly shorter than 3100mAh



And 3400mAh has slightly longer charge time.



My old LiIon cell is handled perfectly at full charge current.



Charging a smaller cell with 0.25mA does, of course, also work.



Charging 4 LiIon batteries at the same time does generate some heat. My probe measures 41°C on the batteries.


M1: 51,5°C, HS1: 77,4°C

The USB port on the back of the charger gets very hot, it is not recommended to touch it.


M1: 50,3°C, HS1: 70,4°C

There is also some hot spots between the batteries and I measure 50°C on the batteries. This is at the limit.




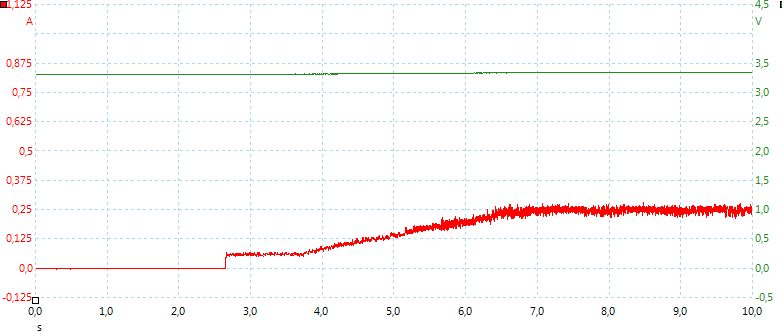
After the charger is powered on it uses about 2 seconds on starting, then 1 second to sense battery type, before ramping up to charge current.



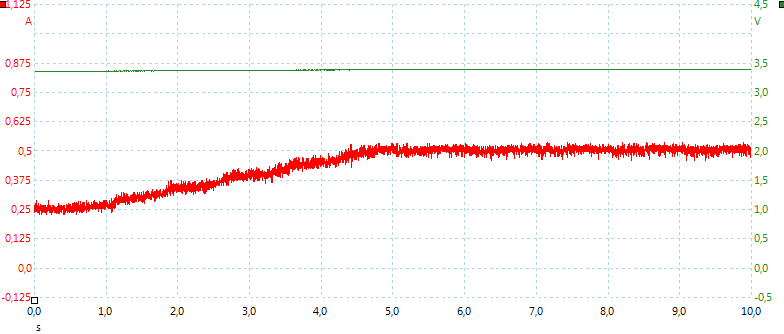
Changing from 0.25A to 0.5A takes about 4 seconds.



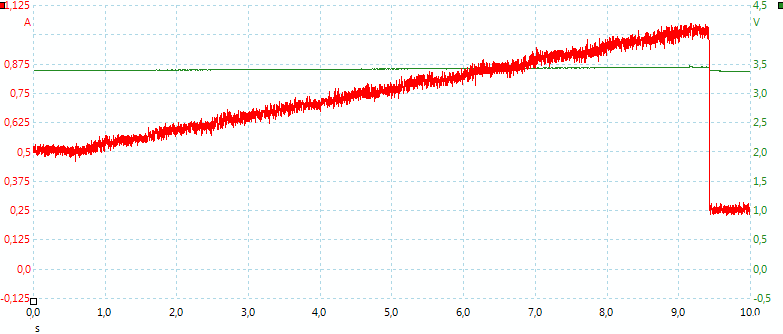
From 0.5A to 1A it takes about 8 seconds to ramp up. Reducing power is instantaneous.
Note: These times are neither good nor bad, it is just the way the charger works.



Test with NiMH cells



A very slow charge of a 2000mAh AA cell and something went wrong. It terminates at 1.40 volt and has only filled 1250mAh into the cell, but then the charge current is too low for this cell, lets test with a AAA cell.
Note: The risk with low charge current is usual overcharge, not premature termination.



Again it terminates early, only about 460mAh has been filled into the cell.



Let’s try 0.5A with a AA cell. Again I get about 1250mAh.
This is not very good.



With a AAA battery at 0.5A the charge is nearly ok.



What about 1A? Again it looks nearly ok, it terminates after about 2000mAh (This is a tad early for a 2000mAh NiMH). When the charge is finished the charger continues with trickle charge.
Notice the slow charge at the start of the curve, it is probably done to detect battery type.





Here are 3. other channels. Looking at the voltage curve, it looks like #2 is terminating slightly early, #3 is good and #4 is early.



With a eneloop XX (2500mAh), the charge curve looks perfect. The voltage has reached a maximum and started to drop, before the charge is terminated.

My guess is that there is a bug in the "end of charge" detection algorithm, this means that it will not work correctly will all types/ages of NiMH batteries. A bit more work from Xtar will probably fit it.



Starting a charge with a full battery, is stopped very fast. First the charger uses two minutes to analyze the battery, then it charges 2½ minutes, before it detects the battery is full and changes to trickle charging.



With 4 batteries, there was also some premature termination, but as can be seen on the temperature curve, that battery did terminate properly. Even with one early termination I recorded a temperature of 51°C
Note: I was measuring volt and current on battery #1 and temperature on battery #3.



Let’s try once more, this time both the battery with voltage/current sensor and the battery with thermo sensor did terminate premature. This time, without proper termination, the temperature did only reach 43°C


M1: 51,1°C, HS1: 74,1°C

The USB port gets very hot with NiMH batteries.


M1: 50,9°C, M2: 51,8°C, M3: 51,2°C, M4: 45,7°C, HS1: 81,9°C

3 batteries at 51°C, the last is charging, but is not as hot.
Somewhere down on the PCB it gets really hot. It is probably not a problem for the electronic parts and it looks like the plastic can take it, but some heat is transferred to the batteries.



In slot #1 the charger can also do a discharge. The battery I tested with was only half full. When charging there was no premature termination. When discharging the led is flashing red.



The current is fairly low, a 2000mAh cell will take nearly 7 hours to discharge and then 2 hours to charge, because the charger only has one slot with discharge function it will take at least 35 hours to cycle a pack of four cells.



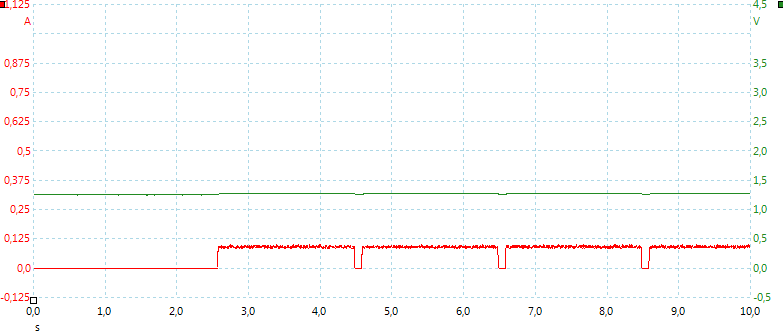
At power on it takes two seconds before the charger starts at the low sense current.



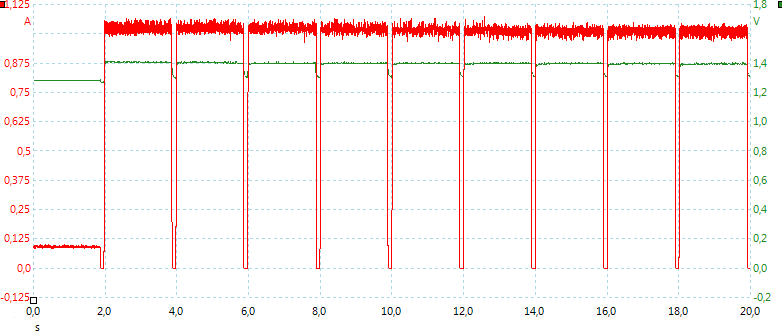
Here it switches from sense to full charge current.



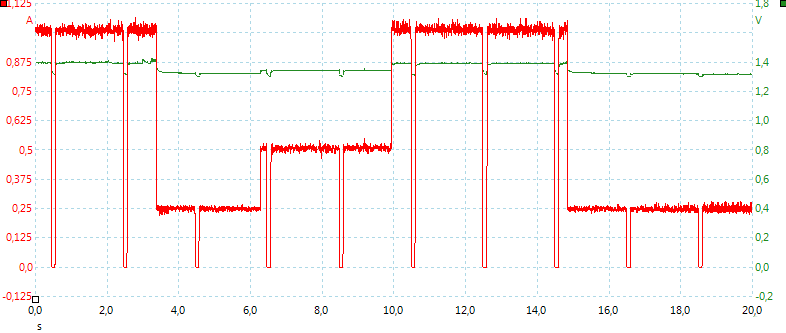
Manual switching between the currents happens instantaneous, with NiMH it does not use a ramp.



Test with both LiIon and NiMH cells



Charging both LiIon and eneloop does not change much. It looks like there is a bit more noise in the charge current.



The NiMH does also look fine.



Measurements USB output

• The charger can only use one battery for the usb output and it has to be a LiIon battery.
• USB out does not turn off when loaded with 200% of rated output
• When battery is empty, the output will be turned off, but there is still drained about 5mA from the battery.
• Output is turned off when battery voltage is slightly above 3 volt, making it useable for all 3.6/3.7 volt LiIon batteries.
• Usb output is coded as Apple 1A

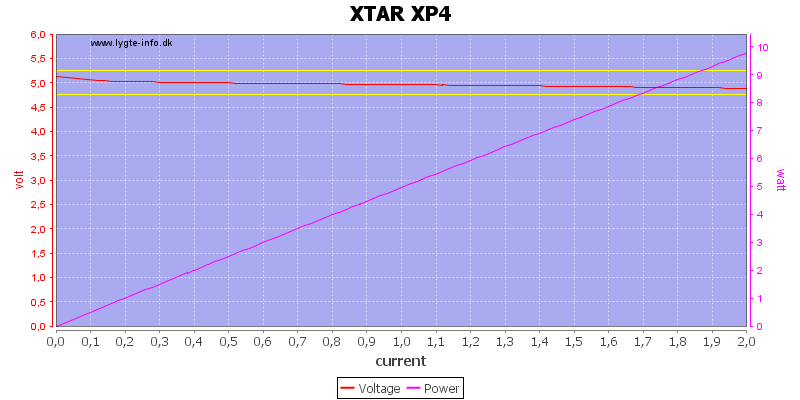
The output is rated at 1A and can easily deliver 2A (To not blow the usb output I stopped at 2A).



At 1A output it has a good efficiency and runs for about 1 3/4 hour. The output turns off when the battery is down to about 3.1 volt, but it still has a current drain of about 5mA from the battery.



Reducing the current to 0.5A improves the efficiency slightly and more than doubles the time it can run.



A 2600mAh gives shorter runtime.



And a 3400mAh gives longer runtime.



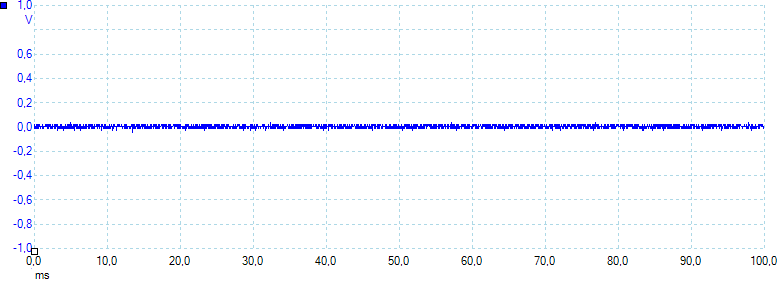
The usb output has very little noise, only about 7mV at 1A (67mVpp).



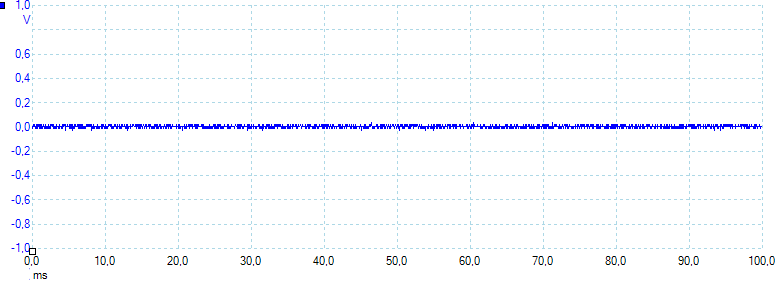
At 0.5A the noise is about the same (6mV and 65mVpp).



Testing with 2500 volt and 5000 volt between mains and low volt side, did not show any safety problems.



Conclusion

The charger has many functions of varying quality:

• The LiIon charger is good and support a wide variety of cell sizes, this is as expected from Xtar.
• The NiMH charger obvious has a bug in the "end of charger" detection and is not very useful.
• The NiMH discharge function is too limited with only one slot and only a slow discharge.
• The USB output delivers very good power, low noise and stable voltage, but do not leave a empty battery in slot #4 for days.
• The charger gets hot while working at maximum current, the battery temperature is just at the allowable limit. I would have preferred both the box and the batteries where considerable cooler, this heat does wear the batteries down faster.

Generally it is a good quad LiIon charger, but the NiMH function is not very good before Xtar get it fixed.



Notes

The charger was supplied by Xtar for a review, I believe it is the second production batch.

Here is an explanation on how I did the above charge curves: How do I test a charger
Read more about how I test USB power supplies and chargers